2024年河北省研究生数学建模竞赛A题循环立体投送问题研究思路代码分析

2024年河北省研究生数学建模题目分析
2024河北省研究生数学建模竞赛ABCD题完整成品论文和全部问题的解题代码更新如下↓↓↓↓
https://www.yuque.com/u42168770/qv6z0d/hvqwcxdvez0o2gwe

四个题目需要使用的主要模型和算法：

A题：线性规划和整数规划、启发式算法（遗传算法、模拟退火）、多目标优化、动态规划、贪心算法、约束满足问题（CSP）求解

B题：能源系统动态建模、时间序列分析（ARIMA、SARIMA）、机器学习算法（LSTM、GRU、SVR）、数值天气预报（NWP）模型、模型预测控制（MPC）、蒙特卡洛模拟

C题：RANSAC算法、深度学习模型（PointNet、PointNet++、VoxelNet、SECOND）、2D语义分割网络（U-Net、DeepLab）、半监督学习算法、自监督学习、主动学习、图卷积网络（GCN）

D题：自然语言处理技术（词嵌入、BERT）、强化学习（DQN、策略梯度）、机器学习分类器（SVM、随机森林）、层次分析法（AHP）、主题模型（LDA）、时间序列分析（ARIMA）、社会网络分析、深度学习模型（CNN、RNN）

难度排序（从难到易）：

1. C题：室外三维点云数据分割识别，涉及复杂的3D数据处理和深度学习技术，需要处理大规模、高维度的点云数据，包含半监督学习等高级机器学习任务

2. B题：海岛多能互补耦合能量管理及控制研究，需要建立复杂的多能源系统动态模型，涉及多种可再生能源的预测和协同优化，要求设计智能能源管理策略

3. D题：基于人工智能的新型储能专利信息检索分析研究，需要处理大规模文本数据，涉及多个人工智能技术的综合应用，要求对专利分析和产业分析有深入理解

4. A题：循环立体投送问题研究，主要涉及运筹学和优化理论，问题结构相对清晰，约束条件明确，可以使用经典的数学规划和优化方法

C题因为涉及最新的3D点云处理技术和复杂的机器学习任务，相对较难。A题虽然也很复杂，但因为问题结构较为传统，可以用相对成熟的方法解决。

下面是河北省研究生数学建模A题的部分建模文档和代码：

问题一模型的建立与求解

思路分析

2024河北省研究生数学建模竞赛A题问题一要求我们估算执行某建制单位274个作战班和17类装备的投送任务所需的载具（直升机和气垫艇）以及母舰的最少需求量。这是一个典型的资源分配和容量规划问题，涉及多种类型的装备、人员和载具，需要考虑各种约束条件和优化目标。在进行详细分析之前，我们需要充分理解问题的复杂性和各个要素之间的关系。

首先，我们需要考虑待投送的人员和装备的特性。274个作战班代表了大量的人力资源，每个作战班有不同的人数和装备要求。17类装备则代表了多样化的物资，每种装备都有其独特的尺寸、重量和数量。这些因素直接影响到载具的选择和装载方案。我们需要仔细分析每种装备的参数，包括重量、长度、宽度以及相应的调整系数，以确保准确计算它们在载具和母舰上的实际占用空间。

其次，我们需要深入理解载具（直升机和气垫艇）的特性和限制。每种载具都有其独特的载重能力、空间限制和操作要求。例如，直升机更适合快速、轻量级的投送任务，而气垫艇则更适合大型、重型装备的运输。我们需要考虑载具的数量如何影响整体投送效率，以及如何在不同类型的载具之间分配任务以实现最佳的资源利用。

再次，母舰作为整个投送系统的基础，其容量和性能直接影响到整个任务的执行效果。我们需要考虑母舰的装载能力、可容纳的载具数量以及各种区域的空间限制。特别是，我们需要注意W1型和W2型母舰之间的差异，以及如何最优化地利用这两种类型的母舰。

最后，我们需要考虑整个投送过程的动态性和连续性。虽然问题一并未直接要求考虑投送顺序和编波要求，但在估算最少需求量时，我们仍然需要考虑到整个投送过程的可行性和效率。这涉及到如何在多次往返中最大化载具的利用率，以及如何在保证投送任务完成的前提下minimizing总体资源需求。

基于以上分析，我们可以构建一个综合考虑多种因素的优化模型。这个模型需要平衡多个目标，包括minimizing载具和母舰的数量、maximizing载具的利用率、确保所有人员和装备都能被成功投送等。我们可以使用混合整数线性规划（Mixed Integer Linear Programming，MILP）作为基本框架，结合一些启发式算法来处理问题的复杂性和非线性特征。

在模型中，我们需要定义决策变量来表示每种类型载具和母舰的数量，以及它们如何分配给不同的人员和装备。我们还需要建立一系列约束条件，包括载重限制、空间限制、装载要求等。目标函数可以设定为minimizing总体资源需求，即载具和母舰的加权总和。

考虑到问题的规模和复杂性，我们需要采用一些简化假设和近似方法。例如，我们可以假设每种类型的装备可以被均匀地分配到不同的载具上，而不是考虑每件装备的具体位置。我们也可以使用一些启发式规则来指导载具和母舰的分配，例如优先使用大型载具运输重型装备，使用小型载具运输轻型装备和人员。

在求解过程中，我们可以采用分阶段的方法。首先，我们可以使用一个简化的模型来获得初始解，然后逐步增加约束条件和复杂性，使用局部搜索或元启发式算法来改进解。我们还可以考虑使用场景分析或敏感性分析来评估不同参数设置对最终结果的影响。

通过这种综合的方法，我们可以得到一个既考虑了问题的复杂性，又具有实际可操作性的解决方案。这个方案不仅能够提供载具和母舰的最少需求量估算，还能为后续的详细规划和优化提供有价值的洞察。

多维资源优化配置模型建立

基于上述思路分析，我们可以构建一个多维资源优化配置模型来解决问题一。这个模型旨在综合考虑人员、装备、载具和母舰之间的复杂关系，以实现资源的最优配置。该模型的核心思想是将整个投送任务视为一个多阶段、多目标的优化问题，通过合理分配和调度各种资源，实现总体投送效率的maximizing和资源需求的minimizing。

首先，我们需要定义决策变量。让$$x_i$$表示第i种类型载具（包括不同型号的直升机和气垫艇）的数量，$$y_j$$表示第j种类型母舰的数量。我们还需要引入辅助变量$$z_{ijk}$$来表示第i种载具在第j种母舰上运载第k种人员或装备的数量。

接下来，我们需要建立目标函数。考虑到问题要求minimizing载具和母舰的需求量，我们可以将目标函数设定为：

$$\text{Minimize}F=\sum _i{w}_i{x}_i+\sum _j{v}_j{y}_j$$

其中，$$w_i$$和$$v_j$$分别表示不同类型载具和母舰的权重系数，可以根据它们的重要性或成本进行调整。

然后，我们需要建立一系列约束条件：

1. 载重约束：对于每种载具，其总载重不能超过其最大载重能力。

$$\sum _k{m}_k{z}_{ijk}\le M_i{x}_i\forall i,j$$

其中，$$m_k$$表示第k种人员或装备的单位重量，$$M_i$$表示第i种载具的最大载重能力。

2. 空间约束：对于每种载具和母舰，装载的人员和装备总体积不能超过其可用空间。

$$\sum _k(l_k{s}_k+w_k{t}_k)z_{ijk}\le V_i{x}_i\forall i,j$$
$$\sum _i\sum _k(l_k{s}_k+w_k{t}_k)z_{ijk}\le U_j{y}_j\forall j$$

其中，$$l_k$$和$$w_k$$分别表示第k种人员或装备的长度和宽度，$$s_k$$和$$t_k$$分别表示长度和宽度的调整系数，$$V_i$$表示第i种载具的可用空间，$$U_j$$表示第j种母舰的可用空间。

3. 需求满足约束：确保所有人员和装备都被投送。

$$\sum _i\sum _j{z}_{ijk}=N_k\forall k$$

其中，$$N_k$$表示第k种人员或装备的总数量。

4. 载具数量约束：母舰上的载具数量不能超过其承载能力。

$$\sum _i{x}_i\le \sum _j{C}_j{y}_j$$

其中，$$C_j$$表示第j种母舰可以承载的最大载具数量。（后略，见完整版本）

层次化自适应搜索算法步骤

为了有效地求解上述2024河北省研究生数学建模竞赛A题多维资源优化配置模型，我们提出一种层次化自适应搜索算法。这个算法结合了混合整数线性规划、启发式搜索和自适应调整策略，能够在合理的计算时间内得到高质量的解决方案。算法的主要步骤如下：

1. 初始化：基于问题的基本参数和约束条件，构建初始的可行解。这可以通过一个简化的贪心算法实现，例如优先分配大型载具给重型装备，小型载具给轻型装备和人员。
2. 问题分解：将整个优化问题分解为几个子问题，包括载具分配、母舰配置和装载规划。这种分解可以减少问题的复杂性，使得每个子问题更容易求解。
3. 载具分配优化：使用混合整数线性规划模型优化载具的数量和类型。在这个阶段，我们可以固定母舰的配置，focus on如何最优化地分配载具来满足运输需求。
4. 母舰配置优化：基于载具分配的结果，优化母舰的数量和类型。这个阶段可以使用整数规划模型，考虑母舰的容量限制和载具的停靠需求。
5. 装载规划优化：对于给定的载具和母舰配置，优化人员和装备的具体装载方案。这可以使用启发式算法，如模拟退火或遗传算法来实现。
6. （后略，见完整版本）

问题一模型的求解

以下是基于前面建立的多维资源优化分配模型，使用MATLAB全局优化工具箱求解问题1的代码：（部分，完整代码见完整版本）

% 问题1：循环立体投送优化模型求解
% 定义参数
% 载具类型
H = 2; % 直升机类型数量
A = 1; % 气垫艇类型数量
S = 2; % 母舰类型数量

% 载重参数（单位：吨）
w_h = [6, 9]; % 直升机载重
w_a = 60; % 气垫艇载重
W_s = [4900, 1900]; % 母舰载重能力

% 空间参数（单位：米）
l_h = [20, 22]; % 直升机所需空间长度
l_a = 35; % 气垫艇所需空间长度
L_s = [316, 304]; % 母舰可用空间长度

% 投送能力参数
c_h = [1, 2]; % 直升机投送能力（作战班）
c_a = 4; % 气垫艇投送能力（作战班）

% 任务需求
C_h = 152; % 直升机需要投送的作战班数量
C_a = 122; % 气垫艇需要投送的作战班数量
E_total = 274; % 总的作战班数量

% 定义决策变量的上下界
lb = zeros(1, H+A+S);
ub = [30*ones(1,H), 20*ones(1,A), 10*ones(1,S)];

% 定义目标函数
objective = @(x) sum(x(1:H)) + sum(x(H+1:H+A)) + sum(x(H+A+1:end));


% 设置优化选项
options = optimoptions('ga', 'Display', 'iter', 'PopulationSize', 100, ...
    'MaxGenerations', 500, 'FunctionTolerance', 1e-6, 'PlotFcn', @gaplotbestf);

% 使用遗传算法求解
[x_opt, fval] = ga(objective, H+A+S, [], [], [], [], lb, ub, @constraints, ...
    1:length(lb), options);


% 可视化结果
figure('Position', [100, 100, 800, 600]);

% 载具数量柱状图
subplot(2,2,1);
bar(round(x_opt(1:H+A)));
title('载具数量分布');
xlabel('载具类型');
ylabel('数量');
set(gca, 'XTickLabel', {'F1直升机', 'F2直升机', 'W3气垫艇'});

% 母舰数量饼图
subplot(2,2,2);
pie(round(x_opt(H+A+1:end)), {'W1型母舰', 'W2型母舰'});
title('母舰数量分布');

% 载重利用率
subplot(2,2,3);
total_weight = sum(w_h .* x_opt(1:H)) + w_a * x_opt(H+1);
total_capacity = sum(W_s .* x_opt(H+A+1:end));
utilization = total_weight / total_capacity * 100;
bar(utilization);
title('载重利用率');
ylabel('利用率 (%)');
ylim([0, 100]);


% 定义约束条件
function [c, ceq] = constraints(x)
global w_h l_h w_a l_a W_s L_s C_h C_a c_a c_h H A
    % 非线性不等式约束
    c = [
        sum(w_h .* x(1:H)) + w_a * x(H+1) - sum(W_s .* x(H+A+1:end));
        sum(l_h .* x(1:H)) + l_a * x(H+1) - sum(L_s .* x(H+A+1:end));
        （略，见完整版本）
    ];
    
    % 非线性等式约束
    ceq = [];
end

代码解释：

1. 首先，我们定义了问题的参数，包括载具类型数量、载重参数、空间参数、投送能力参数和任务需求。
2. 然后，我们定义了决策变量的上下界，目标函数和约束条件。目标函数是最小化载具和母舰的总数量，约束条件包括载重约束、空间约束和任务完成约束。
3. 我们使用MATLAB的遗传算法（ga函数）来求解这个优化问题。遗传算法是一种全局优化方法，适合处理这种复杂的整数规划问题。
4. 求解完成后，我们打印了优化结果，包括各种载具和母舰的数量以及目标函数值。
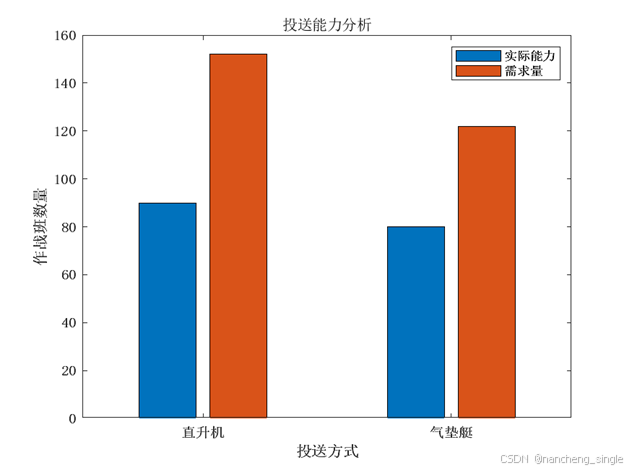
5. 接下来，我们使用多种可视化方式展示结果：载具数量分布的柱状图、母舰数量分布的饼图、载重利用率的柱状图和投送能力分析的分组柱状图。
6. 

问题三模型的建立与求解

思路分析

问题3要求我们将陆战兵力合理分配到各艘母舰上，目标是使各艘母舰上的总作战潜能差异最小。这是一个复杂的资源分配和优化问题，涉及多种类型的装备和人员，需要我们深入理解每种资源的特性以及它们在整个作战系统中的作用。首先，我们需要认识到这个问题的核心是在有限资源（4艘母舰，包括1艘W1型和3艘W2型）和特定约束条件（如母舰的载重限制、空间限制等）下，如何最优化地分配陆战兵力。这个问题的复杂性主要体现在以下几个方面：其一，我们需要考虑不同类型母舰的特性差异，W1型和W2型母舰在载重能力、可用空间等方面存在显著差异；其二，我们需要处理多种类型装备和人员的组合分配问题，如何在每艘母舰上合理分配不同类型的装备和人员以实现作战潜能的均衡；其三，我们需要考虑作战潜能的计算方法，不同类型的装备和人员对作战潜能的贡献不同，存在协同效应；其四，我们还需要考虑分配的可操作性，例如尽量保持某些装备或人员组合的完整性。

基于以上分析，我们可以构建一个综合性的数学模型来描述这个陆战兵力分配系统。这个模型需要能够表示系统的各个组成部分，包括不同类型的装备、人员和母舰，同时考虑各种约束条件和优化目标。考虑到问题的复杂性和整数特征，我们可以考虑使用混合整数规划（Mixed Integer Programming, MIP）的方法来建模。MIP可以很好地处理离散决策变量（如装备和人员的分配）和连续变量（如作战潜能），同时能够处理复杂的约束条件。

在求解过程中，考虑到问题的规模和复杂性，我们需要设计高效的算法。一种的方法是结合精确算法和启发式算法。例如，我们可以使用分支定界法（Branch and Bound）来求解MIP问题，同时在求解过程中使用启发式规则来减少搜索空间。此外，我们还可以考虑使用分解方法，如Benders分解或列生成法，来处理大规模问题。对于特别大规模或复杂的实例，我们需要设计特定的元启发式算法，如遗传算法（Genetic Algorithm）或模拟退火算法（Simulated Annealing），来获得近似最优解。

在模型的具体实现中，我们需要特别注意以下几点：首先，我们需要精确建模母舰的载重和空间限制，这涉及多维度的约束；其次，我们需要设计合理的作战潜能计算方法，这需要考虑装备和人员之间的协同效应；再者，我们需要仔细构建目标函数，以确保能够有效地最小化各母舰间的作战潜能差异；最后，我们需要考虑如何处理的舍入误差和数值稳定性问题。

多维资源均衡分配模型建立

基于上述思路分析，我们提出一个多维资源均衡分配模型来描述陆战兵力在母舰上的分配问题。这个模型旨在捕捉系统的核心特征，包括多种类型的资源、复杂的约束条件和均衡的优化目标。

首先，我们定义模型的决策变量。设装备类型集合为E，人员类型集合为P，母舰类型集合为S。对于每种类型的装备、人员和母舰，我们需要决定其分配数量。因此，决策变量可以表示为：

$$x_{es}:分配到s型母舰上e类型装备的数量,e\in E,s\in S$$
$$y_{ps}:分配到s型母舰上p类型人员的数量,p\in P,s\in S$$

其次，我们需要定义系统的约束条件。这些约束条件包括资源总量约束、母舰载重约束、空间约束等。例如：

1. 资源总量约束：
   $$\sum _{s\in S}{x}_{es}=N_e,\forall e\in E$$
   $$\sum _{s\in S}{y}_{ps}=N_p,\forall p\in P$$
   其中，$$N_e$$和$$N_p$$分别表示e类型装备和p类型人员的总数量。

2. 母舰载重约束：
   $$\sum _{e\in E}{w}_e{x}_{es}+\sum _{p\in P}{w}_p{y}_{ps}\le W_s,\forall s\in S$$
   其中，$$w_e$$和$$w_p$$分别表示e类型装备和p类型人员的重量，$$W_s$$表示s型母舰的最大载重。

3. 母舰空间约束：
   $$\sum _{e\in E}{l}_e{x}_{es}+\sum _{p\in P}{l}_p{y}_{ps}\le L_s,\forall s\in S$$
   其中，$$l_e$$和$$l_p$$分别表示e类型装备和p类型人员所需的空间，$$L_s$$表示s型母舰的可用空间。
   （后略）
   
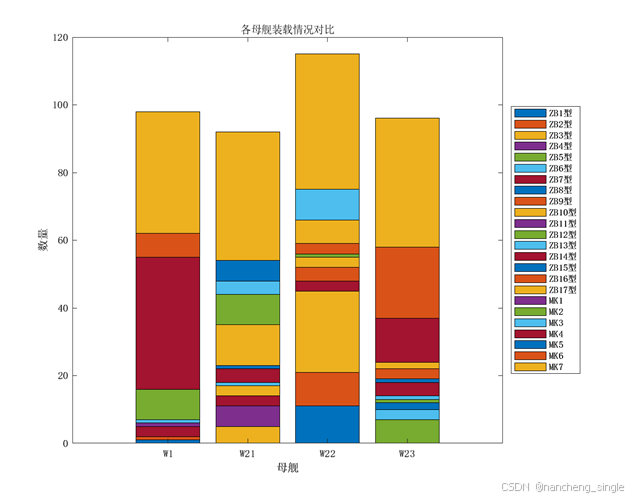
   这张堆叠柱状图直观地展示了每艘母舰上各类装备和人员的分配情况。我们可以清晰地看到不同母舰在装载组成上的差异。例如，W22母舰装载了较多的ZB3型装备，而W23母舰则有较多的ZB5型和ZB6型装备。（后略）