【算法/训练】：动态规划（线性DP）

一、路径类

1. 字母收集

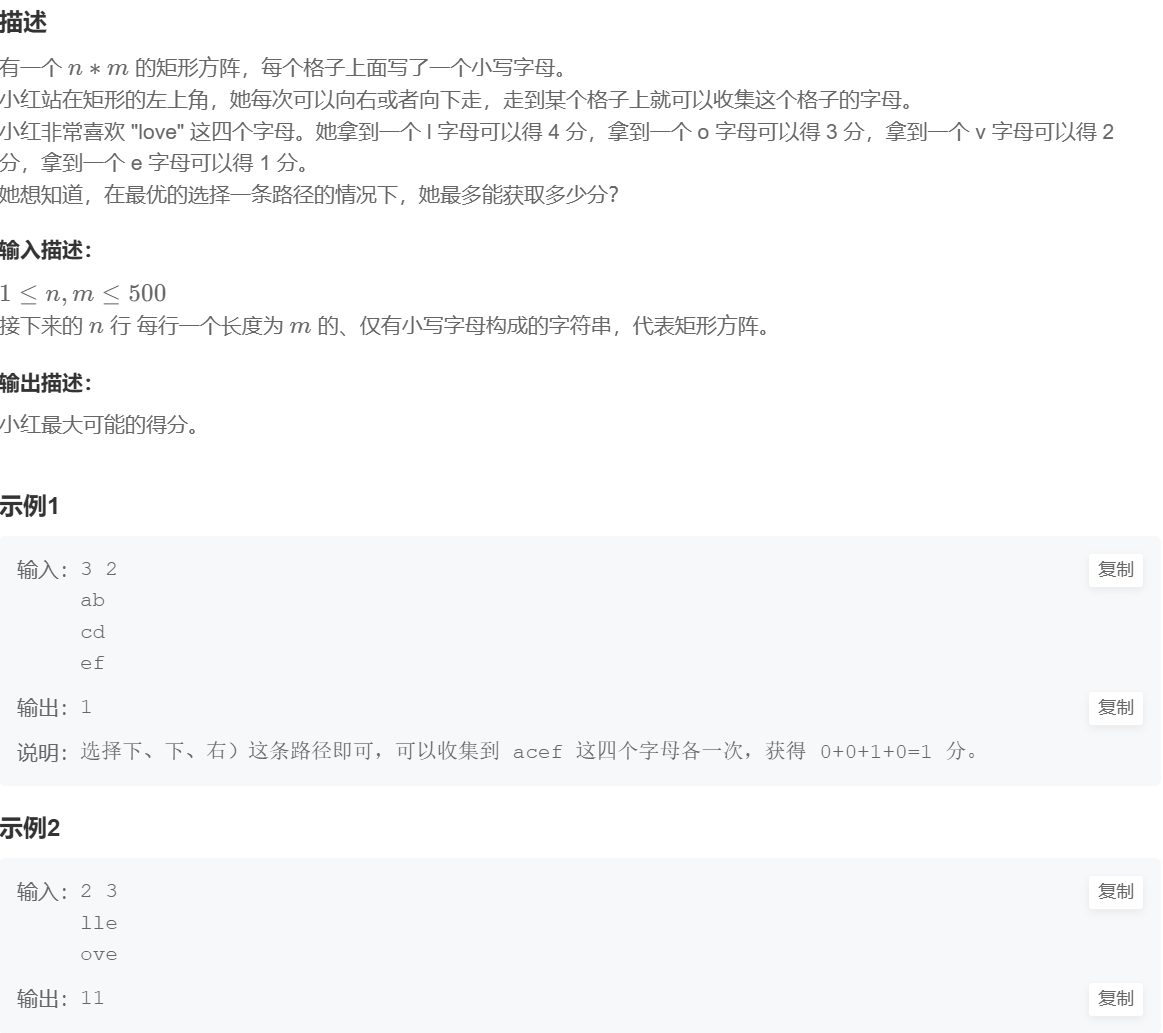
思路：

1、预处理

     对输入的字符矩阵我们按照要求将其转换为数字分数，由于只能往下和往右走，因此走到（i，j）的位置要就是从（i - 1， j）往下走，或者是从(i，j  - 1)的位置往右走，由于我们要使得路程遍历积分最多，则应该从积分多的位置过来，

2、状态表示 dp[i][j] 表示：从[0, 0]出发，到底[i, j]位置，一共有多少分

3、状态转移方程

    故（i，j）位置的积分应该为dp[ i ][ j ] = max(dp[ i - 1 ][ j ], dp[ i ][ j - 1 ]) + dp[ i ][ j ];

4、初始化

    但是上面仅对于（i >= 1 && j >= 1）成立，对于第一行和第一列我们应该特殊处理，利用前缀和的知识可以求得，走到第一列的第i个位置最多能拿的积分以及走到第一行的第j个位置最多能拿的积分，然后我们就可以按照dp[ i ][ j ] = max(dp[ i - 1 ][ j ], dp[ i ][ j - 1 ]) + dp[ i ][ j ]的方法遍历每个节点即可

AC代码如下：

#include <iostream>
using namespace std;

const int N = 1005;
int dp[N][N];

int main() {
	int n, m;
	cin >> n >> m;
	char ch;
	for (int i = 0; i < n; i++){
		for (int j = 0; j < m; j++){
			cin >> ch;
			if (ch == 'l') dp[i][j] = 4;
			else if (ch == 'o') dp[i][j] = 3;
			else if (ch == 'v') dp[i][j] = 2;
			else if (ch == 'e') dp[i][j] = 1;
			else a[i][j] = 0;
		}
	}

for (int i = 1; i < n; i++) dp[i][0] = dp[i - 1][0] + dp[i][0]; 
for (int j = 1; j < m; j++) dp[0][j] = dp[0][j - 1] + dp[0][j]; 

	for (int i = 1; i < n; i++){
		for (int j = 1; j < m; j++){
			dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]) + dp[i][j];
		}
	}

	cout << dp[n - 1][m - 1] << endl;
	return 0;
}

2、[NOIP2002 普及组] 过河卒

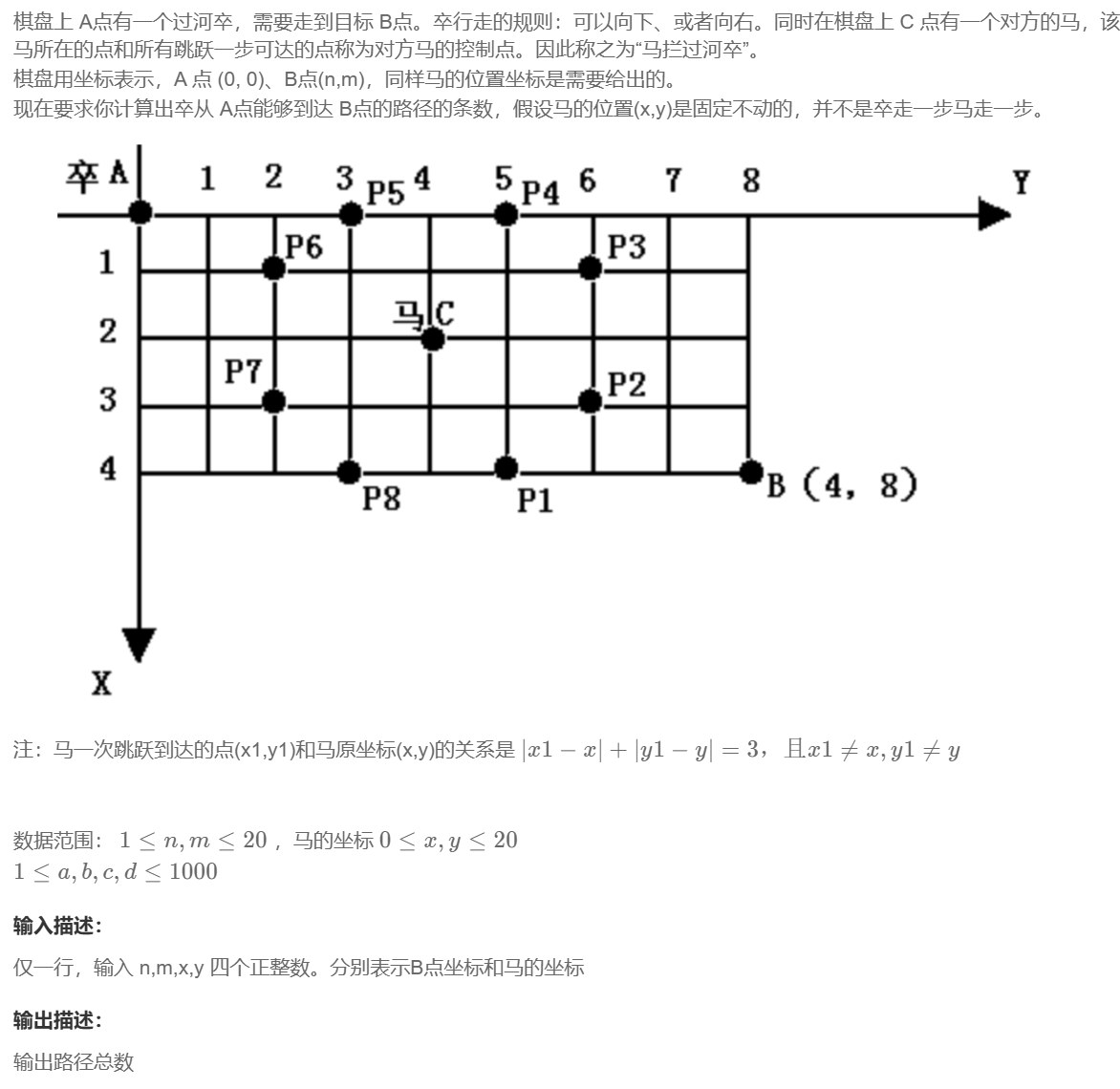
图解：

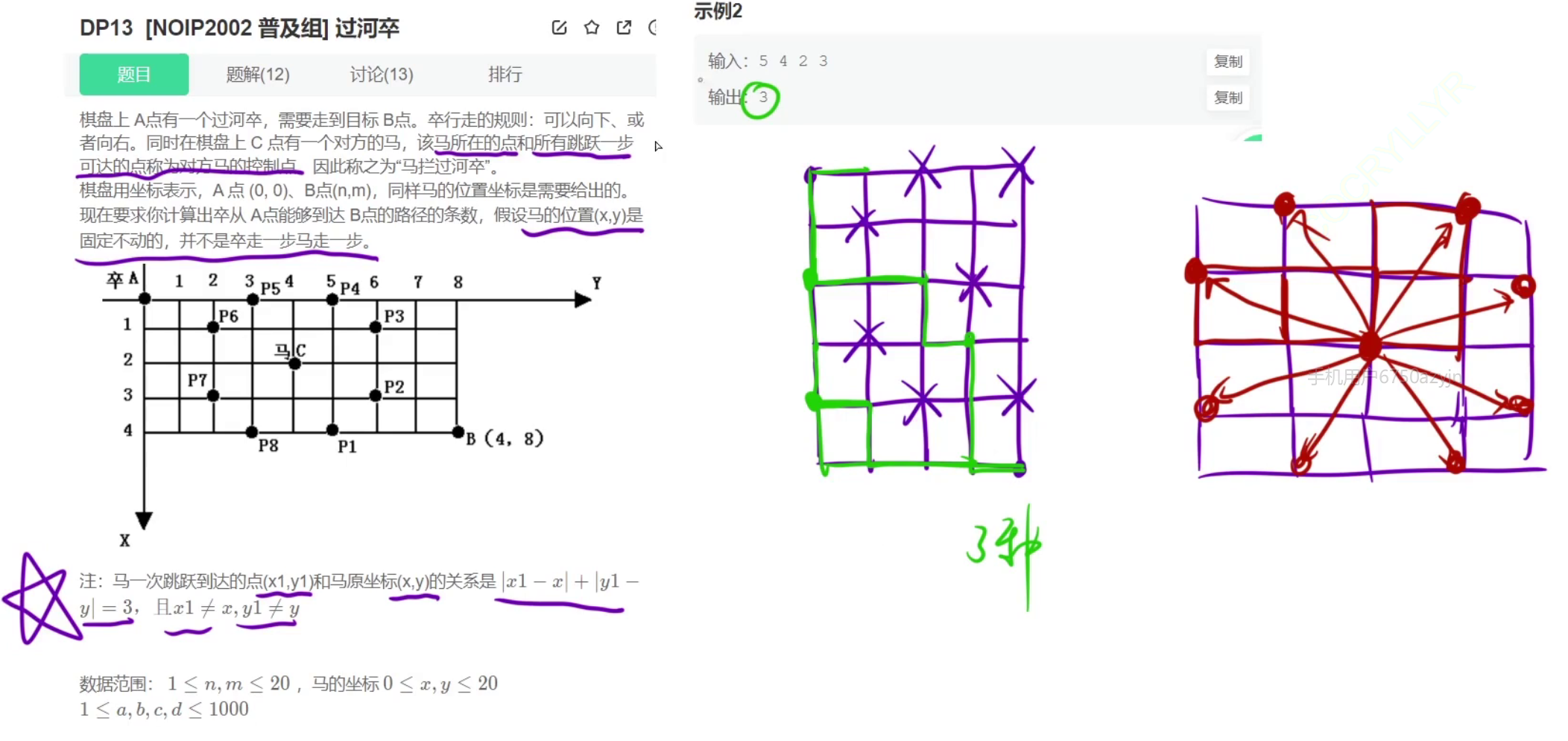
思路：
1、状态表示
dp[i][j] 表示：从[0, 0]出发，到底[i, j]位置，一共有多少种方法
2、状态转移方程

    dp[ i ][ j ] = dp[ i - 1 ][ j ] + dp[i][j - 1] (i > 0 && j > 0)

当走到马可以走的地方，dp[ i ][ j ] = 0;
3、初始化

先创建一个 dp[ n + 2 ][ m + 2 ]，然后让dp[ 0 ][ 1 ] = 1 或者 dp[ 1 ][ 0 ] = 1。注意这样初始化的时候，x需要+1,y也需要+1.和dp表位置一一对应

AC代码如下：

#include <iostream>
#include <vector>
using namespace std;

//int dp[1005][1005];
int main()
{
    int n, m, x, y;
    cin >> n >> m >> x >> y;
    
    vector<vector<long long>> dp(n + 2, vector<long long>(m + 2));
    dp[0][1] = 1;
    x += 1, y += 1;和dp表位置一一对应

    for (int i = 1; i <= n + 1; i++)
    {
        for (int j = 1; j <= m + 1; j++) { //马所在位置
            if (i != x && j != y && abs(i - x) + abs(j - y) == 3 || (i == x && j == y))
            {
                dp[i][j] == 0;
            }
            else dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
        }
    }
    cout << dp[n + 1][m + 1] << endl;

    return 0;
}

3、礼物的最大价值

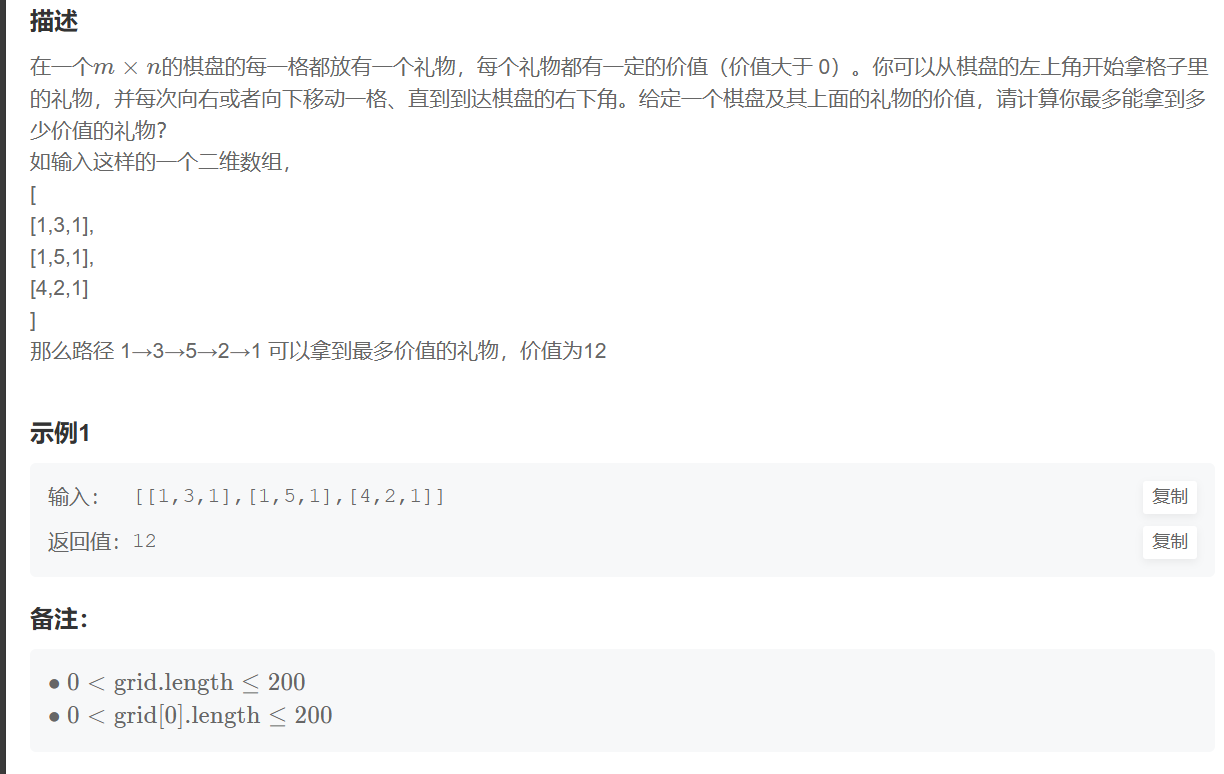
思路：
1、状态表示
dp[i][j] 表示：到[i, j]位置时礼物的最大价值
2、状态转移方程

    dp[ i ][ j ] = max(dp[ i - 1 ][ j ] + w[ i ][ j ]，dp[ i ][ j - 1] + w[ i ][ j ] ）  
3、初始化

我们应该初始化第一行第一列的值，但是我们可以选择多加第一行第一列，把其初始化为0

int maxValue(vector<vector<int> >& grid) {
	int n = grid.size(), m = grid[0].size();
	vector<vector<int>> dp(n + 1, vector<int>(m + 1));
	for (int i = 1; i <= n; i++) {
		for (int j = 1; j <= m; j++) {
			dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]) + grid[i - 1][j - 1];
		}
	}
	return dp[n][m];
}

二、子序列和连续序列类

1. mari和shiny

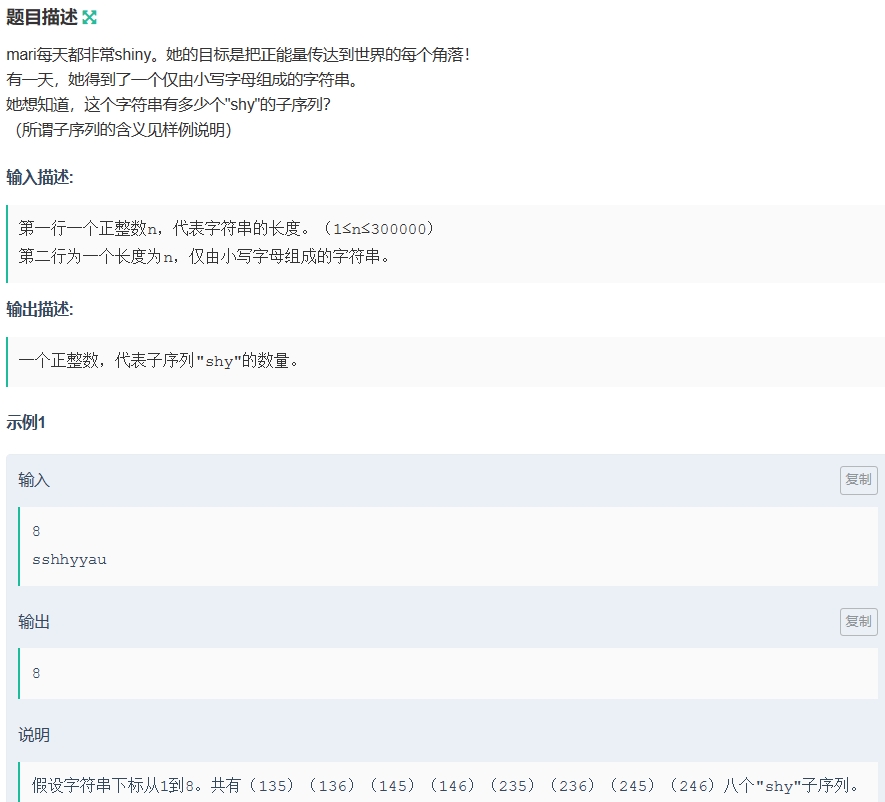
🌈线性 dp

在维护 i 位置之前，⼀共有多少个 "s" "sh" ，然后更新 "shy" 的个数。

（1）状态表示

• s[i]：字符串 str 中 [0, i] 区间内有多少个 "s"。

• h[i]：字符串 str 中 [0, i] 区间内有多少个 "sh"。

• y[i]：字符串 str 中 [0, i] 区间内有多少个 "shy。

---

（2）状态转移方程

---

（3）空间优化

用三个变量来表示即可

s：（字符串 str 中 [0, n-1] 区间内有多少个 "s"）

h：（字符串 str 中 [0, n-1] 区间内有多少个 "sh"）

y：（字符串 str 中 [0, n-1] 区间内有多少个 "shy"）

最后的遍历结束后，y即我们需要的结果

AC代码如下：

#include <iostream>
#include <string>
using namespace std;
typedef long long ll;
int main()
{
	int n;
	string str;
	cin >> n >> str;
	ll s = 0, h = 0, y = 0;
	for (int i = 0; i < n; i++) {
		if (str[i] == 's') s++;
		else if (str[i] == 'h') h += s;
		else if (str[i] == 'y') y += h;
	}
	cout << y << endl;
	return 0;
}

🌈二维 dp 

这道题目如果不是子序列，而是要求连续序列的，那就可以考虑用 KMP。

（1）dp[i][j] 含义

• string t="shy"

dp[i][j]：以 i-1 为结尾的 str 子序列中出现以 j-1 为结尾的 t 的个数为 dp[i][j]。

---

（2）递推关系

• str[i - 1] 与 t[j - 1]相等
• str[i - 1] 与 t[j - 1] 不相等

当 str[i - 1] 与 t[j - 1]相等时，dp[i][j] 可以有两部分组成：

1. 一部分是用 str[i - 1] 来匹配，那么个数为 dp[i - 1][j - 1]。即不需要考虑当前 str 子串和 t 子串的最后一位字母，所以只需要 dp[i-1][j-1]。
2. 一部分是不用 str[i - 1] 来匹配，个数为 dp[i - 1][j]。

为什么还要考虑不用 str[i - 1] 来匹配，都相同了指定要匹配？
🧩例如： str：shyy 和 t：shy ，str[3] 和 t[2] 是相同的，但是字符串 str 也可以不用 str[3] 来匹配，即用 str[0]str[1]str[2] 组成的 "shy"。当然也可以用 str[3] 来匹配，即：str[0]str[1]str[3] 组成的 "shy"。

所以，当 str[i - 1] 与 t[j - 1] 相等时，dp[ i ][ j ] = dp[ i - 1 ][ j - 1 ] + dp[ i - 1 ][ j ];

当 str[i - 1] 与 t[j - 1] 不相等时，dp[i][j] 只有一部分组成，不用 str[i - 1] 来匹配（就是模拟在 str 中删除这个元素），即：dp[i - 1][j]，所以递推公式为：dp[ i ][ j ] = dp[ i - 1 ][ j ];

为什么只考虑 “不用 str[i - 1] 来匹配” 这种情况， 不考虑 “不用 t[j - 1] 来匹配” 的情况呢？
🧩这里要明确，我们求的是 str 中有多少个 t，而不是求 t 中有多少个 str，所以只考虑 str 中删除元素的情况，即不用 str[i - 1] 来匹配 的情况。

---

（3）状态转移方程

• dp[i][j]显然要从dp[i-1][?]递推而来。立即思考dp[i-1][j], dp[i-1][j-1]分别与dp[i][j]的关系。因为少一个字符，自然而然从当前字符着手。考察si的第i个字符(表为s[i])和tj的第j个字符(表为t[j])的关系。

• 若s[i] ≠ t[j]：那么s_i中的所有t_j子序列，必不包含s[i]，即s_i-1和s_i中tj的数量是一样的，得到该情形的转移方程： dp[ i ][ j ] = dp[ i -1 ][ j ]

• 若s[i] = t[j]：假设s_i中的所有t_j子序列中，包含s[i]的有a个，不包含的有b个。s_i中包含s[i]的子序列个数相当于s_i-1中t_j-1的个数，不包含s[i]的子序列个数与上一种情况一样，于是得到该情形的转移方程：

  a = dp[ i -1 ][ j -1 ] b = dp[ i-1 ][ j ] dp[ i ][ j ] = a + b = dp[i-1][j-1] + dp[i-1][j]

---

（4）遍历顺序

从上到下，从左到右。

AC代码如下：

#include <iostream>
#include <vector>
 
using namespace std;
 
int main()
{
    int n;
    cin >> n;
    string str;
    cin >> str;
    string t="shy";
    int m=t.size();
 
    vector<vector<long long>> dp(n+1, vector<long long>(m+1));
    for(int i=0; i<=n; i++) dp[i][0]=1;
 
    for(int i=1; i<=n; i++)
    {
        for(int j=1; j<=m; j++)
        {
            if(str[i-1]==t[j-1])
                dp[i][j]=dp[i-1][j-1]+dp[i-1][j];
            else
                dp[i][j]=dp[i-1][j];
        }
    }
 
    cout << dp[n][m] << endl;
 
    return 0;
}

2. 不同的子序列

该题于上题不一样的是，上面给定了t的具体字符串，而这里没有给定，但是我们也需要用二维dp的方法来写。

（1）dp[i][j] 含义

s[ i ]的子序列中在t[ j ]出现的次数

s[ i ]表示s从下标 i 到末尾的子字符串。

t[ j ]表示t从下标 j 到末尾的子字符串。

---

（2）递推关系

1. 分别令两个维度为0，推测边界。
2. dp[0][j]表示s_0中t_j的个数。s_0是空字符串，只有当j=0时，才有dp[0][j] = 1，表示s子空串中有一个t子空串，否则dp[0][j] = 0，因为一个空串不可能包含一个非空串。

3. dp[i][0]表示s_i中t0的个数。t_0是空字符串，显然任何串（包括空串）都含有一个空子串。因此dp[i][0] = 1。

4. 注意到，dp[i][0] = 1实际上已经包含了dp[0][j] = 1的情形。

---

（3）初始化

• dp[i][0] 表示：以 i-1 为结尾的 str 可以随便删除元素，出现空字符串的个数。所以，dp[i][0] 一定都是 1，因为也就是把以 i-1 为结尾的 str，删除所有元素，出现空字符串的个数就是 1。
• dp[0][j] 表示：空字符串 str 可以随便删除元素，出现以 j-1 为结尾的字符串 t 的个数。所以，dp[0][j] 一定都是 0，因为 str 如论如何也变成不了 t。
• dp[0][0] 表示：空字符串 str 可以删除 0 个元素，变成空字符串 t。所以，dp[0][0] = 1。

---

（4）遍历顺序

从上到下，从左到右。

AC代码如下： 

​
int numDistinct(string s, string t) {
	int n = s.size(), m = t.size();
	if (n < m) return 0;
	vector<vector<unsigned int>> dp(n + 1, vector<unsigned int>(m + 1)); //注意是unsigned int
	for (int i = 0; i <= n; i++) dp[i][0] = 1;
	for (int i = 1; i <= n; i++) {
		for (int j = 1; j <= m; j++) {
			dp[i][j] = dp[i - 1][j] +(s[i - 1] == t[j - 1] ? dp[i - 1][j - 1] : 0);
		}
	}
	return dp[n][m];
}

​

3. 连续子数组最大和

思路：
1、状态表示
dp[ i ]表示：以 i 位置为结尾的所有子数组中的最大和

方法一：
2、状态转移方程

对于nums[i]有两种情况:一种是和前一个位置的子序列连着dp[i]=dp[i-1]+nums[i]
第二种是以自己独立门户，从自己开始dp[i]=nums[i]

取其中最大值,可得状态转移方程为 dp[ i ] =  max(dp[i - 1] + nums[i], nums[i]) ;

3、初始化

dp[0]=nums[0]

方法二：

2、状态转移方程

 dp[ i ] = max(dp[ i - 1 ] ， 0） + nums[ i - 1 ] .
3、初始化

dp[ 0 ] = 0，然后从下标1开始计算，最后返回 dp 表的最大值即可

AC代码如下：

#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;

int main() {
	int n;
	cin >> n;
	vector<int> dp(n + 1);
	int w, ret = -101;
	for (int i = 1; i <= n; i++) {
		cin >> w;
		dp[i] = max(dp[i - 1], 0) + w;
		ret = max(ret, dp[i]);
	}
	cout << ret << endl;
	return 0;
}

4、最长回文子序列

思路：
1、状态表示

dp[ i ][ j ] 表示：字符串[ i，j] 区间内最长回文子序列的长度
2、状态转移方程

1. i > j 时，dp[ i ][ j ] = 0;
2. i = j 时，dp[ i ][ j ] = 1;
3. i < j，分以下两种情况

• s[ i ] = s[ j ]时候，dp[ i + 1][ j - 1]  +2;
• s[ i ] != s[ j ]时候，max(dp[i - 1][ j ]，dp[ i ][ j - 1] )

3、初始化

dp[ 0 ] = 0，然后从下标1开始计算，最后返回 dp 表的最大值即可

 AC代码如下：

int longestPalindromeSubSeq(string s) {
	// write code here
	int n = s.size();
	vector<vector<int>> dp(n, vector<int>(n));
	//i为起始索引，j为结束索引
	for (int i = n - 1; i >= 0; i--) {
		dp[i][i] = 1;
		for (int j = i + 1; j < n; j++) {
			//相同，则加2
			if (s[i] == s[j])
				dp[i][j] = dp[i + 1][j - 1] + 2;
			//不同，则从dp[i+1][j] dp[i][j-1]中寻找最大值。
			else
				dp[i][j] = max(dp[i + 1][j], dp[i][j - 1]);
		}
	}
	return dp[0][n - 1];
}

三、偷盗问题

1. 打家劫舍

思路：

首先考虑最简单的情况。如果只有一间房屋，则偷窃该房屋，可以偷窃到最高总金额。如果只有两间房屋，则由于两间房屋相邻，不能同时偷窃，只能偷窃其中的一间房屋，因此选择其中金额较高的房屋进行偷窃，可以偷窃到最高总金额。如果房屋数量大于两间，应该如何计算能够偷窃到的最高总金额呢？

方法一：二维

1、状态表示

设 dp[i][0] 为不偷第 i 个房间的情况下，前 i 个数偷盗总金额的最大值；dp[i][1]为取第 i 个数的情况下，前 i 个数不偷盗总金额的最大值。

2、状态转移方程

不偷当前房间，那么前一个房间取不取都行：

dp[i][0]=max(dp[i−1][1],dp[i−1][0])

若取当前房间，那么前一个房间一定不能取：

dp[i][1]=dp[i−1][0]+ nums[i - 1]

最后需要输出 max(dp[n][0],dp[n][1])

方法二：一维

对于 k（ k > 2）的房屋数量，有两个选项：

• 偷窃第k间房屋，那么就不能偷窃第 k−1 间房屋，偷窃总金额为前 k−2 间房屋的最高总金额与第 k 间房屋的金额之和。

• 不偷窃第 k 间房屋，偷窃总金额为前 k−1 间房屋的最高总金额。

  在两个选项中选择偷窃总金额较大的选项，该选项对应的偷窃总金额即为前 k 间房屋能偷窃到的最高总金额。

1、状态表示
dp[ i ]：表示前i间房屋能偷盗的最多钱数。
2、状态转移方程

    dp[ i ] = max(dp[ i - 2 ] + nums[ i ] , dp[i - 1] )

提示里说了nums.length>=1;

对于nums.length==1，需特殊处理，return nums[0];

AC代码如下：

int rob(vector<int>& nums) {
	int n = nums.size();

	// 方法一：二维表示
	/*vector<vector<int>> dp(n + 1, vector<int>(n + 1));
	for (int i = 1; i <= n; i++)
	{
		dp[i][0] = max(dp[i - 1][0], dp[i - 1][1]);
		dp[i][1] = dp[i - 1][0] + nums[i - 1];
	}
	return max(dp[n][0], dp[n][1]);*/

	//方法二：一维表示
	/*if (n == 1) return nums[0];
	vector<int> dp(n + 1);
	dp[0] = nums[0];
	dp[1] = max(nums[0], nums[1]);
	for (int i = 2; i < n; ++i) {
		dp[i] = max(dp[i - 2] + nums[i], dp[i - 1]);
	}
	return dp[n - 1];*/

	//方法三：再优化
	int f1 = 0, f0 = 0;
	for (int i = 0; i < n; i++) {
		int tmp = max(f1, f0 + nums[i]);
		f0 = f1;
		f1 = tmp;
	}
	return f1;
}

2. 打家劫舍 II

思路：

    这道题中的房屋是首尾相连的，第一间房屋和最后一间房屋相邻，因此第一间房屋和最后一间房屋不能在同一晚上偷窃。和上题相似，这道题也可以使用动态规划解决。

考虑是否偷 nums[0]：

• 如果偷 nums[0]，那么 nums[1] 和 nums[n−1] 不能偷，问题变成从 nums[2] 到 nums[n−2] 的非环形版本。
• 如果不偷 nums[0]，那么问题变成从 nums[1] 到 nums[n−1] 的非环形版本。
• 分别取 [start,end)=[2,n−2) 和 [start,end)=[1,n−1) 进行计算，取两个 dp[end] 中的最大值，即可得到最终结果

假设偷窃房屋的下标范围是 [start,end]，用 dp[i] 表示在下标范围 [start,i] 内可以偷窃到的最高总金额：

1、状态表示
   dp[ i ]：表示前i间房屋能偷盗的最多钱数。
2、状态转移方程

    dp[i]=max(dp[i−2]+nums[i],dp[i−1])

注意：这题我们用 tmp, f1, f0 来分别表示dp[i]，dp[i - 1]，dp[i -2]。 

AC代码如下：

int robRange(vector<int>& nums, int start, int end) { // [start, end) 左闭右开
    int f1 = 0 , f0 = 0;
    for (int i = start; i < end; i++) {
        int tmp = max(f1, f0 + nums[i]);
        f0 = f1;
        f1 = tmp;
    }
    return f1;
}

int rob(vector<int>& nums) {
    int n = nums.size();
    return max(nums[0] + robRange(nums, 2, n - 1), robRange(nums, 1, n));
}

3. 打家劫舍 III

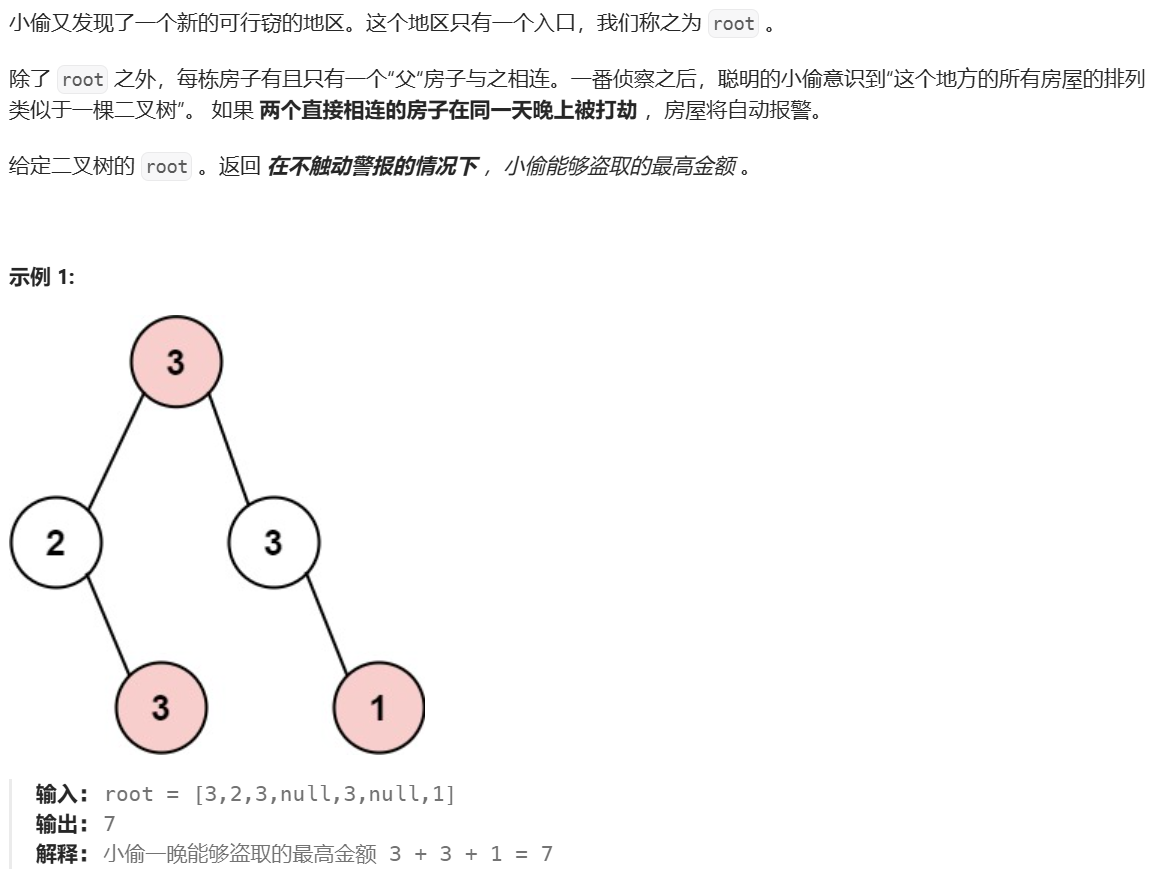
思路：

对于当前节点，就两个选择，抢或者放弃。然后我们用 f(o) 表示抢 o 节点的情况下，o 节点的子树上被选择的节点的最大权值和；g(o) 表示不抢 o 节点的情况下，o 节点的子树上被选择的节点的最大权值和；l 和 r 代表 o 的左右孩子。

🧩1、当 o 被选中时，o 的左右孩子都不能被选中，故 o 被选中情况下子树上被选中点的最大权值和为 l 和 r 不被选中的最大权值和相加，即 f(o)=g(l)+g(r)。
🧩2、当 o 不被选中时，o 的左右孩子可以被选中，也可以不被选中。对于 o 的某个具体的孩子 x，它对 o 的贡献是 x 被选中和不被选中情况下权值和的较大值。故 g(o)=max{f(l),g(l)}+max{f(r),g(r)}。
🧩至此，我们可以用哈希表来存 f 和 g 的函数值，用深度优先搜索的办法后序遍历这棵二叉树，我们就可以得到每一个节点的 f 和 g。根节点的 f 和 g 的最大值就是我们要找的答案。

AC代码如下：

unordered_map<TreeNode*, int>f, g;
void dfs(TreeNode* node)
{
	if (node == nullptr) return;
	dfs(node->left), dfs(node->right);
	f[node] = node->val + g[node->left] + g[node->right]; //如果抢该节点
	g[node] = max(f[node->left], g[node->left]) + max(f[node->right], g[node->right]);
}


int rob(TreeNode* root) {
	dfs(root);
	return max(f[root], g[root]);
}

4. 打家劫舍 IV

思路：

     通过观察可以发现，当偷盗能力越大时，小偷最多能偷的房屋数就越多；如果偷盗能力越小时，小偷最多能偷的房屋数就越少。

     由题意我们可知，这是求最小的最大值，因此我们可以想到用二分的方法来找到合适的 capacity。对于每个通过二分列举出来的 capacity，因为碍于偷盗能力，小偷只能偷价值不超过 capacity 的房子，而且不能连续偷。因此，我们可以通过动态规划的方法算出：当小偷的偷盗能力为 capacity 时，小偷可以最多可以偷多少间房（设为 y），如果 y >= k，那么就代表 capacity 偏大，要把 capacity 调小一点；如果 y < k，那么就代表 capacity 偏小，把 capacity 调大一点。且由于要求的是最小的最大值，因此属于二分里面的区间左端点问题。

处。

     通过二分枚举 capacity，对每个 capacity 进行动态规划，求出在该 capacity 的情况下最多偷到的房屋数，然后再根据这个房屋数调整 capacity 的查找区间。

AC代码如下：

int minCapability(vector<int>& nums, int k) {
    vector<int> capacity = nums;
    sort(capacity.begin(), capacity.end());

    int l = 0, r = capacity.size() - 1;
    while (l < r)
    {
        int m = (r - l >> 1) + l; //注意：+， -的优先级高于>>
        if (check(nums, capacity[m]) >= k)r = m;
        else l = m + 1;
    }
    return capacity[l];
}

int check(vector<int>& nums, int capacity)
{
    int n = nums.size();
    vector<vector<int>> dp(n + 1, vector<int>(2));

    for (int i = 1; i <= n; i++)
    {
        if (nums[i - 1] <= capacity) dp[i][1] = dp[i - 1][0] + 1;
        dp[i][0] = max(dp[i - 1][1], dp[i - 1][0]);
    }
    return max(dp[n][1], dp[n][0]);
}

 

四、背包问题

1. 01背包问题

1、状态表示

dp[ i ][ j ]表示：从前 i 个物品中挑选，总体积不超过j，此时最大的重量

2、状态转移方程

dp[ i ][ j ] = max (dp[i - ][ j ]  (不选i)， dp[i - 1][ j - v[ i ]] + w[ i ]  (选i) ) 

3、初始化问题 dp[ 0 ][ j ]  = 0 ;

4、 返回dp[n][V].

5、空间优化

dp[ j ] = max ( dp [ j ], dp[ j - v[ i ] + w [ i ] ]  

AC代码如下：

#include <iostream>
using namespace std;

const int N = 1005;
int dp[N], v[N], w[N];

int main() {
    int n, V;
    cin >> n >> V;
    for (int i = 1; i <= n; i++) cin >> v[i] >> w[i]; //体积权重
    for (int i = 1; i <= n; i++)  { //体积
        for (int j = V; j >= v[i]; j--) { //逆序，表示该物品最多使用一次
            dp[j] = max(dp[j], dp[j - v[i]] + w[i]);
        }
    }
    cout << dp[V] << endl;
    return 0;
}

2. 完全背包问题

思路：

和上题不同的是，01背包中n件物品只能使用一次，而这里可以无限次使用

那么我们可以把这题把多次使用的某件物品看作多次插入，那么这道题的解题步骤就和上面类似了，状态转移方程也基本和上面类似，我们这里同样也进行了空间优化。

上一篇代码中，我们用的是逆序是为了保证更新当前状态时，用到的状态是上一轮的状态，保证每个物品只有一次或零次;
在这里，因为每个物品可以取任意多次，所以不再强求用上一轮的状态，即本轮放过的物品，在后面还可以再放;

AC代码如下：

#include <iostream>
using namespace std;

const int N = 1010;
int dp[N],v[N], w[N];

int main(){
    int n, V;
    cin >> n >> V;
    for (int i = 1; i <= n; i++) cin >> v[i] >> w[i];

    for (int i = 1; i <= n; i++){
        for (int j = v[i]; j <= V; j++){
            dp[j] = max(dp[j], dp[j - v[i]] + w[i]);
        }
    }
    cout << dp[V] << endl;
    return 0;
}

3. [NOIP2001]装箱问题

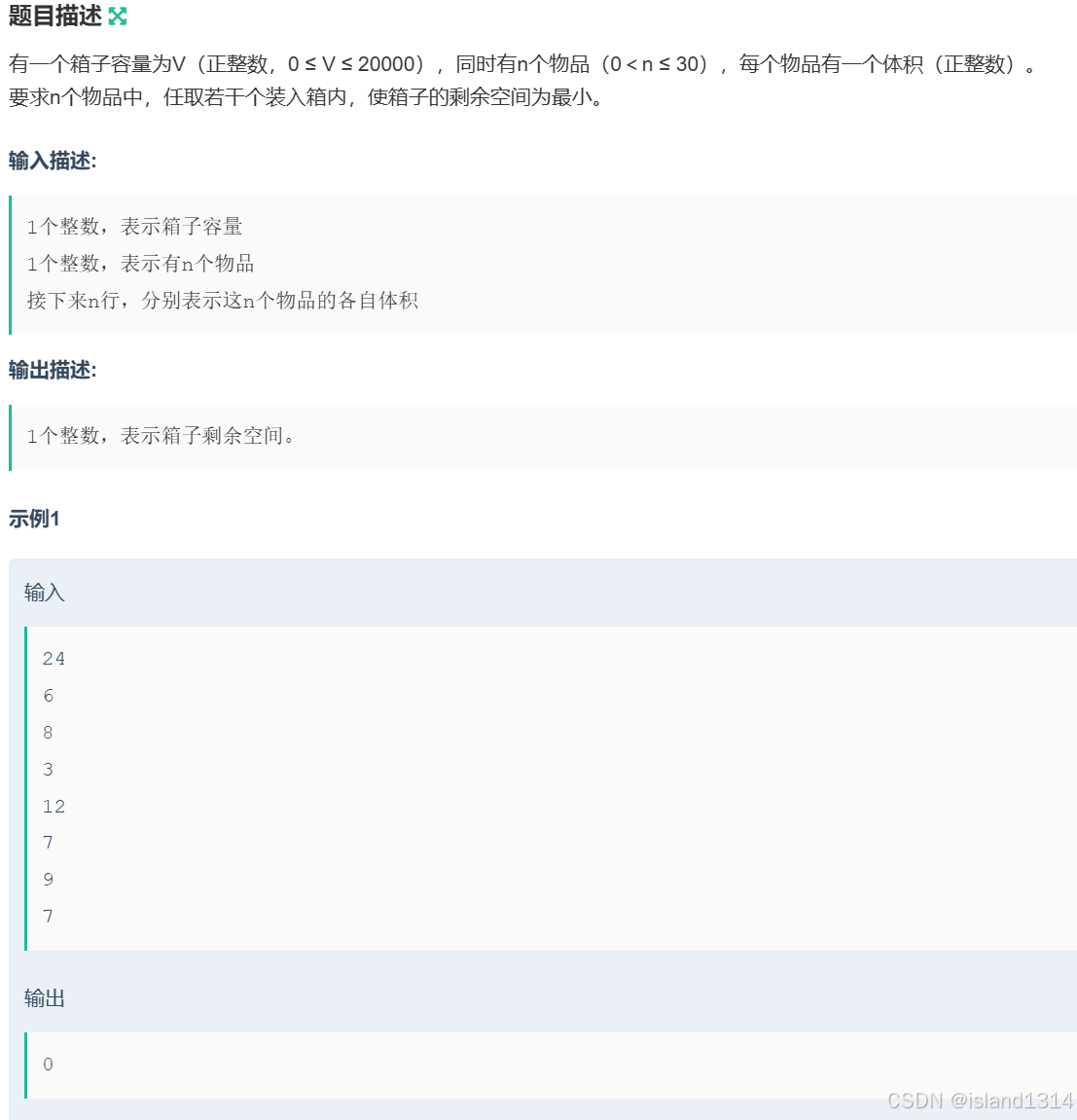
思路：

该题也是个典型的01背包问题

1、状态表示
dp[i][j] 表示：从前 i 个物品中挑选，总体积不超过 j，此时的最大体积
2、状态转移方程

    dp[ i ][ j ] = max(dp[ i - 1 ][ j ] ，dp[ i ][ j - V[ i ]] + V[ i ]) （j >= arr[ i ]）
3、初始化

返回 V - dp[ n ][ V ]

AC代码如下：

const int N = 35, M = 2e4 + 10;
int v[N], dp[N][M];

void solve3(){
	int V, n;
	cin >> V >> n;
	for (int i = 1; i <= n; i++) cin >> v[i];
	for (int i = 1; i <= n; i++) 
	{
		for (int j = 0; j < V; j++)
		{
			dp[i][j] = dp[i - 1][j];
			if (j >= v[i])
				dp[i][j] = max(dp[i][j], dp[i - 1][j - v[i]] + v[i]);
		}
	}

	cout << V - dp[n][V] << endl;
}

4. 分割等和子集

思路：

该题也是个典型的01背包问题

1、状态表示
dp[i][j] 表示：从前 i 个数字中挑选，总和恰好为 j，看是否能够凑成，因此我们这的dp数组为bool类型
2、状态转移方程

第一种：最后一个数不选，先从前i - 1个数中挑，因为最后一个不选，对总和不造成影响，

如果我们从前 i - 1种情况能凑成j，那么在从前 i种情况肯定能凑成j

第二种：选了第i个数字，那从前i - 1个数中挑，对总和会造成影响，因此我们应该在前i - 1个数中凑总和为 j - arr[ i ]即可

    dp[ i ][ j ] = dp[ i - 1 ][ j ] || dp[ i ][ j - arr[ i ]] （j >= arr[ i ]）
3、初始化

在之前的dp表基础上多加一行多加一列，方便我们初始化，初始dp[0][0] = true.

4、返回值

返回dp[ n ][ sum / 2] 即可

注：如果总和为奇数，永远都选不出来一半，直接返回false即可。

AC代码如下：

#include <iostream>
#include <algorithm>
using namespace std;

const int N = 505, M = 505 * 110 / 2;
bool dp[N][M];
int arr[N];

int main()
{
	int n;
	cin >> n;
	int sum = 0;
	// 1.计算总和
	for (int i = 1; i <= n; i++) {
		cin >> arr[i];
		sum += arr[i];
	}

	// 2.判断总和是否为奇数，为奇数直接截止
	if (sum % 2 == 1) {
		cout << "false" << endl;
		return 0;
	}

	// 3.动态规划
	sum /= 2;
	dp[0][0] = true; //初始化
	for (int i = 1; i <= n; i++)
	{
		for (int j = 0; j <= sum; j++) {
			dp[i][j] = dp[i - 1][j]; //当i = 0，j = 0的初始化
			if(j >= arr[i])
				dp[i][j] = dp[i - 1][j] || dp[i][j - arr[i]];
		}
	}
	if (dp[n][sum]) cout << "true" << endl;
	else cout << "false" << endl;

	return 0;
}