ACM_前缀和算法

欢迎来到@一夜看尽长安花博客，您的点赞和收藏是我持续发文的动力

对于文章中出现的任何错误请大家批评指出，一定及时修改。有任何想要讨论的问题可联系我：3329759426@qq.com 。发布文章的风格因专栏而异，均自成体系，不足之处请大家指正。

专栏：

java全栈
C&C++
PythonAI
PCB设计
Linux云计算&运维

文章概述：ACM算法 ——前缀和算法

关键词：ACM 一维前缀和二维前缀和

本文目录：

前缀和

一维前缀和

原理

公式（思想）

运算逻辑（前缀和算法的目的）

示例：

二维前缀和

原理：

公式：

运算逻辑

大家注意：

示例：

前缀和

主要是个思想或者说是个公式

一维前缀和

原理

原数组

前缀和数组

公式（思想）

运算逻辑（前缀和算法的目的）

求得 [ r, l ]之间的原数组元素之和（区间和）

将前r项a数组的和Sr 减去前l-1项和S l-1 , 得到的是第【r,l】之间的数组元素之和

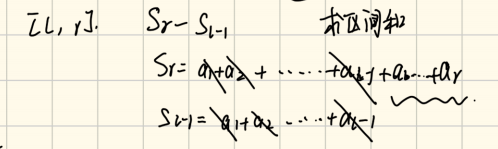
示例：

#include <iostream>

using namespace std;

const int N=100010;

int n,m;
//初始化数组
int a[N],s[N];

int main()
{
    scanf("%d%d",&n,&m);
    for(int i = 1;i<=n;i++) scanf("%d",&a[i]);

    for(int i = 1;i<=n;i++) s[i]=s[i-1]+a[i]; //前缀和的初始化

    while(m--)
        {
            int l,r;
            scanf("%d%d",&l,&r);
            printf("%d\n",s[r]-s[l-1]); //区间和的计算
        }

    return 0;
}

二维前缀和

原理：

和一维类似，我们用图片的形式，方便大家理解

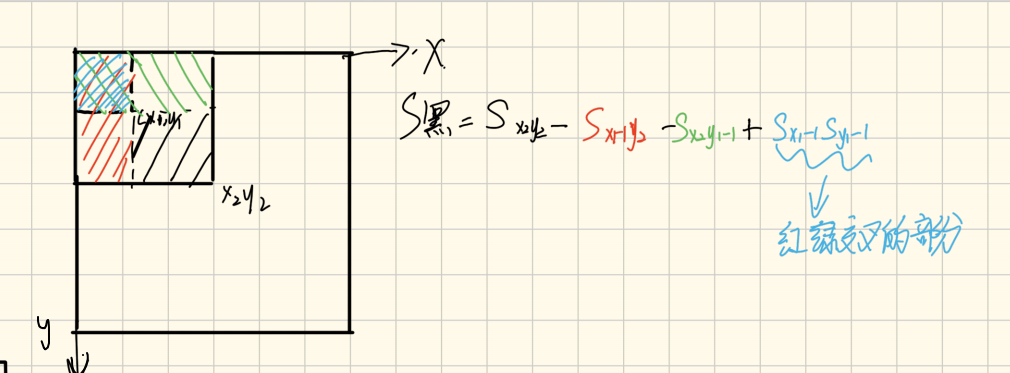
a本身是个矩阵，求矩阵中部分区间的元素和即为二维前缀和

就是求黑色区间的元素和，图中给大家陈列出了公式

公式：

四个整数 x1,y1,x2,y2，表示子矩阵的左上角和右下角

运算逻辑

还是用图形的形式，让大家更容易理解

求前缀和：

求子矩阵（矩阵中只含有单个元素）

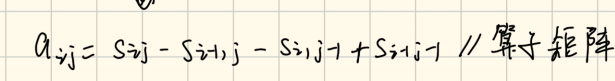
大家注意：

1.求前缀和都是从从下标1开始的，然后分别用我们一维前缀和里的公式和二维的公式推到结果

2.这个大家也是不用考虑边界问题的，因为我取得下标没有重合，

比如求区间 [ l , r ] ,就是S r - S l-1

示例：

#include <iostream>

using namespace std;

const int N = 1010;

//传入三个参数  n行，每行包含 m个整数，表示整数矩阵。
//接下来 q行，表示一组询问 每次询问包含四个整数 x1,y1,x2,y2，表示矩阵的左上角和右下角
int n, m, q;
//初始化
int s[N][N];

int main()
{
    scanf("%d%d%d", &n, &m, &q);
	
	//获取原矩阵
    for (int i = 1; i <= n; i ++ )
        for (int j = 1; j <= m; j ++ )
            scanf("%d", &s[i][j]);
		
	//前缀和公式（前缀和的初始化）
    for (int i = 1; i <= n; i ++ )
        for (int j = 1; j <= m; j ++ )
            s[i][j] += s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1];
		
	//求区间（子矩阵）和
    while (q -- )
    {
        int x1, y1, x2, y2;
        scanf("%d%d%d%d", &x1, &y1, &x2, &y2);
        printf("%d\n", s[x2][y2] - s[x1 - 1][y2] - s[x2][y1 - 1] + s[x1 - 1][y1 - 1]);
    }

    return 0;
}